Adrienne L. Erickcek

My research focuses on how we can use cosmological observations to learn about inflation, dark matter and dark energy. I have studied how the transition from inflation to radiation domination can affect the small-scale distribution of dark matter and how the observed hemispherical asymmetry in the cosmic microwave background could have been generated during inflation. I have also investigated how gravitational lensing can be used to detect local dark matter clumps and how gravitational measurements within the Solar System constrain new gravity theories that are designed to eliminate the need for dark energy. I have also explored how these modified gravity theories behave in the early Universe.
 

Here are brief descriptions of my major research projects. I have tried to make these descriptions accessible to readers who do not have a background in cosmology. For those in search of more information (and equations), I have included links to the technical papers associated with each project. You can also look at my publication list if you want to learn more about my research, including my work on projects not highlighted here. Finally, I have given presentations on these topics, and slides are available here.

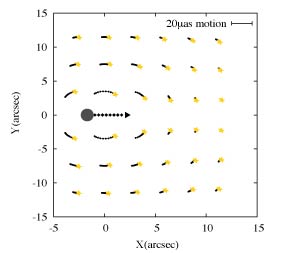
Chameleon Gravity in the Early Universe

Probes of the Primordial Power Spectrum

Substructure from Reheating

From the abundance of helium and deuterium in the Universe, we know that the Universe was once filled with a hot plasma; it was radiation dominated. Other observations suggest that the Universe was not radiation dominated from its birth; during inflation, the Universe was dominated by the inflaton. To make the hot plasma that was the setting for the production of primordial helium and deuterium, the inflaton had to decay. Between the end of inflation and inflaton decay, the Universe was effectively matter dominated. The Universe may also have been effectively matter dominated for some time after the inflaton decayed. All we know is that eventually the Universe became radiation dominated, and when it became radiation dominated, it had a temperature of at least 10¹⁰ Kelvin. The onset of radiation domination is called reheating.

We showed that a period of matter domination prior to reheating leaves a distinctive imprint on the amplitude of density fluctuations on scales smaller than the cosmological horizon at reheating. The fluctuations in the radiation density on these small scales are suppressed compared to the fluctuations on larger scales that entered the horizon after reheating. If the dark matter interacted strongly with radiation after reheating, small scale density fluctuations in the dark matter will be similarly suppressed. Any substructure on scales smaller than the horizon at reheating will be erased, leading to a minimum mass for dark matter subhalos.

We also considered the possibility that the dark matter may be a decay product of the matter-like substance that dominated the Universe before reheating. In this case, the dark-matter density perturbations on small scales are enhanced. Density fluctuations on scales that enter the horizon before reheating grow quickly until the Universe becomes radiation dominated, and after reheating, the dark matter produced from decays inherits these density fluctuations. This early growth gives small-scale density fluctuations a head start compared to larger fluctuations, and they collapse to form halos much earlier. Consequently, a large fraction of the dark matter is contained in small dense clumps in this scenario. These clumps may be as large as a few earth-masses, and they would probably survive within our galaxy.

In summary, our work shows that we can learn about the state of the Universe prior to reheating by studying dark matter substructure. In particular, the presence or absence of small dark matter clumps within our galaxy can give us information about when reheating happened, the origin of dark matter, and how the dark matter interacted with radiation after reheating.

back to top

Gravitational Lensing by Nearby Dark Matter Subhalos

High resolution simulations of galaxy-sized dark matter halos, like the Aquarius and Via Lactea simulations indicate that the dark matter within the Milky Way is not uniformly distributed. Rather, there are numerous dark matter subhalos within the Milky Way; these subhalos contain more that 10000 solar masses of dark matter, and they can be found deep within the galaxy.

The only thing we know about dark matter is that it has gravitational pull. Therefore, a dark matter subhalo can bend the light from stars that lie behind it; it is a gravitational lens. As the subhalo moves across the sky, the bending of the starlight changes, and the image of the star

appears to move, as illustrated here. The gray circle is the center of the dark matter subhalo (the full subhalo would cover the picture). Over the course of four years, a typical subhalo fifty parsecs away moves about four arcseconds, as shown by the arrow. The stars near the subhalo center start at the position of the yellow stars, and over the next four years, their images move to the left, as shown by the black dots. In this figure, the stars' motions are exaggerated compared to their positions; the scale bar shows twenty microarcseconds of image motions.

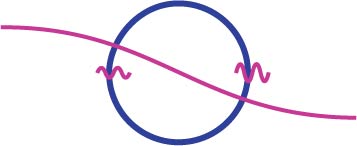
These are tiny image motions; a microarcsecond is roughly the width of a nickel held on the Moon. Nevertheless, it is possible to observe such tiny changes in stellar positions through the use of high-precision astrometry. We evaluated the region of the sky that is detectably lensed by a dark matter subhalo given different levels of astrometric precision. We found that it is unlikely to find a subhalo through its astrometric lensing; the subhalos are too rare and they each lens too small a region of sky to have a significant chance of seeing a lensing event with a survey instrument like Gaia. However, the Fermi Gamma-Ray Space Telescope measures localized gamma-ray emission consistent with dark matter self-annihilation, then astrometric gravitational lensing can be used to determine if the source is really a dark matter subhalo.

back to top

Asymmetric Inflation

The cosmic microwave background (CMB) has an intriguing and unexpected feature: the average fluctuation amplitude in one half of the sky is about 10% larger than the average amplitude on the other half of the sky. This fluctuation power asymmetry was first found by Eriksen et al., and it is significant at the 99% confidence level.

We proposed that this power asymmetry could be produced by a very large-amplitude and long-wavelength perturbation in the energy density of the Universe during inflation. Such a perturbation would effectively make the mean energy density on one side of the Universe larger than the mean energy density on the other side. Since the mean energy density determines the amplitude of the energy fluctuations, the long wavelength mode would create a power asymmetry just like the asymmetry observed in the CMB.

This picture illustrates our mechanism for generating a power asymmetry during inflation. The blue sphere represents the CMB sky around us, while the pink curves represent the energy

density during inflation. The long-wavelength mode changes the background value, making it asymmetrical. The short-wavelength fluctuations, also shown in pink, have different amplitudes on different sides of the sky because they are fluctuations in different backgrounds.

Unfortunately, our mechanism for generating the power asymmetry has an unwelcome side effect that we describe in the second paper in this series. The long-wavelength fluctuation will change the mean temperature of the CMB in addition to changing the amplitude of the small-wavelength fluctuations. We calculated how such long-wavelength fluctuations create temperature fluctuations in the CMB, and we found that the near-uniformity of the CMB temperature limits how much the mean energy density may vary from one side of the sky to the other. These limits rule out our original model, which assumed that the inflaton was the only type of energy present during inflation. Instead, we were forced to postulate that there was a second type of energy during inflation and that inhomogeneities in this secondary energy source led to the power asymmetry observed in the CMB sky.

If the secondary field that causes the power asymmetry is also responsible for all the observed inhomogeneities in the CMB, then the power asymmetry should be equally present on all scales. After we proposed our model for the power asymmetry, Chris Hirata showed that small-scale density fluctuations are not as asymmetric as the larger-scalar fluctuations probed by the CMB. In the third paper, we show that a exclusively large-scale power asymmetry can be generated if the secondary field decays into dark matter, leading to asymmetric fluctuations in the ratio of dark matter particles to photons. These "isocurvature" fluctuations cannot explain all the observed inhomogeneities in the CMB, so in this model, most of the fluctuations come from the inflaton. This explanation for the CMB power asymmetry predicts that the Planck satellite will detect isocurvature perturbations in the CMB.

back to top

Solar System Tests of f(R) Gravity

Given the strangeness of dark energy, it is reasonable to wonder if the cosmic acceleration may be a sign that our understanding of gravity is flawed. While Einstein's theory of general relativity has passed every test we have given it, all of those tests are necessarily confined to the borders of the Solar System. It is possible that galaxies are accelerating away from each other because gravity behaves differently between galaxies than it does between the planets and the Sun.

How can we modify gravity so that galaxies accelerate apart? One possibility is to replace the Lagrangian of general relativity, which is simply the Ricci curvature scalar R, with some function of the Ricci curvature scalar f(R). This modification is called f(R) gravity, and there are several types of f(R) gravity that will drive cosmic acceleration.

The problem with f(R) gravity is that it is very difficult to change how gravity behaves between galaxies without changing how it behaves in the Solar System. Moreover, while there is only one spherically symmetric vacuum solution to the gravitational equations in general relativity, there are many such solutions in f(R) gravity. To determine how f(R) gravity will behave locally, you have find the particular solution that corresponds to our Solar System, and this subtlety generated some confusion regarding whether or not f(R) gravity was consistent with tests of general relativity.

In the first paper in this series, we showed that one form of f(R) gravity, known as 1/R gravity, is incompatible with Solar System gravitational tests and is therefore ruled out. We then generalized our calculation to other forms of f(R) gravity in the second paper. We found that all forms of f(R) gravity that satisfy a few simple conditions are incompatible with Solar System tests and are not viable alternatives to dark energy. One of these conditions demands that the value of the Ricci scalar does not deviate much from its vacuum value. Forms of f(R) gravity that do not satisfy this condition can mimic general relativity inside the Solar System and are currently under investigation as possible alternatives to dark energy.

back to top

Solar System Tests of Chern-Simons Gravity

Chern-Simons gravity is a modification of general relativity that adds a new term to the gravitational action. The new term is higher-order in the curvature and violates parity, which means that Chern-Simons gravity behaves differently when viewed in a mirror.

Chern-Simons gravity is interesting for two reasons. First, it is a simple example of a gravitational theory that is parity-violating. Since other fundamental forces are known to violate parity, it is interesting to test whether or not gravity is parity-violating. Studying Chern-Simons gravity tells us where to look for parity-violating gravitational effects. Second, the new term that is added to the general relativity action in Chern-Simons gravity is a common feature of low-energy effective gravitational theories derived from string theory.

Chern-Simons gravity is very difficult to distinguish from general relativity because the differences between the two theories only emerge in systems that are not spherically symmetric. Consequently, there were no constraints on Chern-Simons gravity prior to our work. We derived the Chern-Simons gravitational effects due to the Earth's rotation, and we showed that these effects would slightly alter the orbits of satellites. We were able to use the orbits of the LAGEOS satellites to place the first constraints on the parameters of Chern-Simons gravity, and we noted that these constraints will be significantly improved by Gravity Probe B.

back to top

SMBH Mergers and Halo Merger Theory

The merger of two supermassive black holes (SMBHs) is expected to produce a gravitational-wave signal detectable by the satellite LISA. The rate of SMBH mergers is intimately connected to the galaxy merger rate, and the extended Press-Schechter formalism is often employed when calculating the rate at which these events will be observed. This merger theory is flawed and provides two rates for the merging of the same pair of galactic haloes.

An alternate merger rate proposed by Andrew Benson, Marc Kamionkowski, and Steven Hassani (BKH) may be obtained directly from the Press-Schechter halo mass function. We calculated the SMBH merger event rate using both versions of the extended Press-Schechter formalism and a preliminary version of the BKH merger rate.

We found that the SMBH merger event rate is dominated by mergers of galaxies with nearly equal masses; consequently, the two versions of the extended Press-Schechter merger rate give nearly equal SMBH merger rates. However, the preliminary BKH merger rate leads to a SMBH merger event rate that is thirty percent lower than the event rate derived from the extended Press-Schechter formalism.

back to top