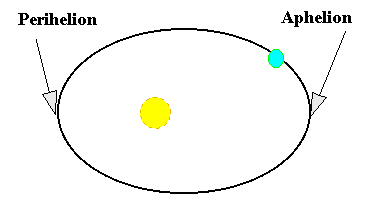
The point at which a planet or asteroid
is closest to the sun is called PERIHELION. The point at which it is farthest is
called APHELION.Kepler's Second Law
(The line joining the Sun and a planets sweeps out equal areas in equal times)
The JAVA Applet below demonstrates this law. Press Continue to start the planet orbitting. Press Start Sweeping to begin the planet sweeping. Press Stop Sweeping when you think it has gone a good distance. Press Start Sweeping again a little later in the orbit. It will automatically sweep for as long as you did the first time. You can see (and it shows you in the table along the bottom) that the area swept out was equal both times. Press Erase Areas to try it again. You may want to increase the eccentricity so that the effect is more pronounced.
Notice that both the DISTANCE of a planet from the sun and the SPEED at which the planet moves changes during the orbit. If equal areas are swept out in equal times, then since the sides of the sector vary as the planet orbits (since its distance from the Sun changes), the speed at which the planet travels changes, since the planet must cover a different distance in its path in the same amount of time (and SPEED = DISTANCE/TIME).
Answer questions 2-2.1 and 2-2.2 on the worksheetThe point at which a planet or asteroid
is closest to the sun is called PERIHELION. The point at which it is farthest is
called APHELION.
Newtonian mechanics can be used to calculate the speed of the planet at various points along its orbit. If P is the planet’s orbital period, and a is the semimajor axis, then the orbital speed V at perihelion and aphelion are given by:
at perihelion and
at aphelion
For the Earth, we have a = 1 A.U. = 1.496 x 108 km
P = 1 yr = 3.156 x 107 sec
e = 0.0167
Calculate the orbital velocity of the Earth at perihelion and aphelion, and record the answers as 2-2.3 on the worksheet
Return to Previous Part of Lab | Continue to Next Part of the Lab