(absolute) uncertainty - the amount (often stated in the form ± d x) that along with the measured value, indicates the range in which the desired or true value most likely lies [Baird, 14]. The total uncertainty of a value [Fluke, G-3]. The error [Taylor, 14]. (Taylor does not distinguish between the terms error and uncertainty.)
relative (fractional) uncertainty - the absolute uncertainty divided by the measured value, often expressed as a percentage or in parts per million (ppm) [Taylor, 28; Baird, 14].
standard uncertainty, ui – the uncertainty of the result of a measurement expressed as a standard deviation [ISO, 3].
combined standard uncertainty, uc(y) – the standard deviation of the result of a measurement when the result is obtained from the values of a number of other quantities. It is obtained by combining the individual standard uncertainties ui (and covariances as appropriate), using the law of propagation of uncertainties, commonly called the "root-sum-of-squares" or "RSS" method. The combined standard uncertainty is commonly used for reporting fundamental constants, metrological research, and international comparisons of realizations of SI units [ISO, 3].
Type A evaluation of standard uncertainty – method of evaluation of uncertainty by the statistical analysis of a series of observations [ISO, 3].
Type B evaluation of standard uncertainty – method of evaluation of uncertainty by means other than the statistical analysis of series of observations [ISO, 3].
precision - the degree of consistency and agreement among independent measurements of a quantity under the same conditions [Fluke, G-11]. Indicated by the uncertainty [Bevington, 2], or the fractional (relative) uncertainty [Taylor, 28]. The degree of refinement with which an operation is performed or a measurement stated [Webster]. Precision is a measure of how well the result has been determined (without reference to a theoretical or true value), and the reproducibility or reliability of the result. The fineness of scale of a measuring device generally affects the consistency of repeated measurements, and therefore, the precision. The ISO has banned the term precision for describing scientific measuring instruments because of its many confusing everyday connotations [Giordano, 1997 #2301].
accuracy (of measurement) [VIM 3.5] – closeness of agreement between a measured value and a true value [ISO, 33; Fluke, G-3; Bevington, 2; Taylor, 95]. The term "precision" should not be used for "accuracy" [ISO, 33]. A given accuracy implies an equivalent precision [Bevington, 3]. Freedom from mistake or error, correctness; degree of conformity of a measure to a standard or a true value [Webster].
true value (of a quantity) [VIM 1.19] - value consistent with the definition of a given particular quantity. A true value by nature is indeterminate; this is a value that would be obtained by a perfect measurement [ISO, 32]. The correct value of the measurand [Fluke, G-15]. The value that is approached by averaging an increasing number of measurements with no systematic errors [Taylor, 130].
Note: The indefinite article "a," rather than the definite article "the," is used in conjunction with "true value" because there may be many values consistent with the definition of a given particular quantity [ISO, 32]. (This distinction is not clear in other references that refer to "the true value" of a quantity.)
result of a measurement [VIM 3.1] - value attributed to a measurand, obtained by measurement. A complete statement of the result of a measurement includes information about the uncertainty of measurement [ISO, 33].
error (of measurement) [VIM 3.10] - result of a measurement minus a true value of the measurand (which is never known exactly); sometimes referred to as the "absolute error" to distinguish from "relative error" [ISO, 34]. Deviation from the "true" or nominal value [Bevington, 5; Fluke, G-7]. The inevitable uncertainty inherent in measurements, not to be confused with a mistake or blunder [Taylor, 3]. The amount of deviation from a standard or specification; mistake or blunder [Webster]. (Students often cite "human error" as a source of experimental error.)
random error [VIM 3.13] - result of a measurement minus the mean that would result from an infinite number of measurements of the same measurand carried out under repeatable conditions [ISO, 34]. Statistical fluctuations (in either direction) in the measured data due to the precision limitations of the measurement device [Fluke, G-12; Taylor, 94]. Random errors can be reduced by averaging a large number of observations: standard error = s /sqrt(n) [Taylor, 103].
systematic error [VIM 3.14] - mean that would result from an infinite number of measurements of the same measurand carried out under repeatability conditions minus a true value of the measurand; error minus random error [ISO, 34]. A reproducible discrepancy between the result and "true" value that is consistently in the same direction [Baird, 14; Fluke, G-14]. A reproducible inaccuracy introduced by faulty equipment, calibration, or technique [Bevington, 3, 14]. These errors are difficult to detect and cannot be analyzed statistically [Taylor, 11]. Systematic error is sometimes called "bias" and can be reduced by applying a "correction" or "correction factor" to compensate for an effect recognized when calibrating against a standard. Unlike random errors, systematic errors cannot be reduced by increasing the number of observations [ISO, 5].
mistake or blunder - a procedural error that should be avoided by careful attention [Taylor, 3]. These are illegitimate errors and can generally be corrected by carefully repeating the operations [Bevington, 2].
discrepancy - a significant difference between two measured values of the same quantity [Taylor, 17; Bevington, 5]. (Neither of these references clearly defines what is meant by a "significant difference," but the implication is that the difference between the measured values is clearly greater than the combined experimental uncertainty.)
relative error [VIM 3.12] - error of measurement divided by a true value of the measurand [ISO, 34]. (Relative error is often reported as a percentage. The relative or "percent error" could be 0% if the measured result happens to coincide with the expected value, but such a statement suggests that somehow a perfect measurement was made. Therefore, a statement of the uncertainty is also necessary to properly convey the quality of the measurement.)
significant figures - all digits between and including the first non-zero digit from the left, through the last digit [Bevington, 4]. (e.g. 0.05070 has 4 significant figures.)
decimal places – the number of digits to the right of the decimal point. (This term is not explicitly defined in any of the examined references.)
standard error (standard deviation of the mean) – the sample
standard deviation divided by the square root of the number of data points:
SE or SDM = ![]() where
where ![]() is the sample variance [Taylor, 102].
is the sample variance [Taylor, 102].
(The ISO Guide and most statistics books use the letter s to represent the sample standard deviation and s (sigma) to represent the standard deviation of the population; however, s is commonly used in reference to the sample standard deviation in error analysis discussions, i.e. x ± 2s )
margin of error - range of uncertainty. Public opinion polls generally use margin of error to indicate a 95% confidence interval, corresponding to an uncertainty range of x ± 2s [Taylor, 14].
coverage factor, k – numerical factor used as a multiplier of the combined standard uncertainty in order to obtain an expanded uncertainty. Note: k is typically in the range 2 to 3 [ISO, 3; Fluke 20-6].
(e.g. If the combined standard uncertainty is uc = 0.3 and a coverage factor of k = 2 is used, then the expanded uncertainty is Uc = kuc = 0.6)
law of propagation of uncertainty - the uncertainty sz of a quantity z = f(w1, w2, …, wN) that depends on N input quantities w1, w2, …, wN is found from
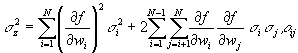
where si2 is the variance of wi and rij is the correlation coefficient of the covariance of wi and wj. If the input quantities are independent (as is often the case), then the covariance is zero and the second term of the above equation vanishes. The above equation is traditionally called the "general law of error propagation," but this equation actually shows how the uncertainties (not the errors) of the input quantities combine [ISO, 46; Bevington, 43; Taylor, 75].